Towers of Hanoi with a small modification.

This problem is taken from Jeff Erickson’s Algorithms ‘textbook’, link here. This is Problem 3 from the first chapter which is on Recursion. This has been shortened considerably.

You’re given three needles/pegs lettered A,B & C from left to right. You have \(n\) disks placed on peg A and you’re goal is to move all \(n\) disks from A to C with the following restrictions

1. You can only move disks one at a time onto peg B or from/to Peg A and C.
2. It is forbidden to place a larger disk onto a smaller one.
3. You can move any number of disks from peg B to any other peg.

The problem is to describe the algorithm and the number of steps it takes i.e. the Running time.

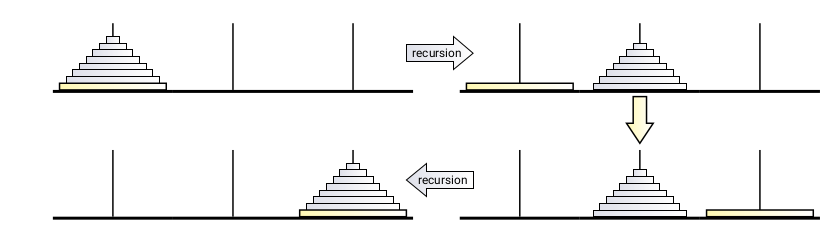
I was assisted by this figure below -

The important clue here is that with the restriction number three, we have only one recursive sub-problem instead of the usual two in the classical Tower of Hanoi problem. Say that you begin with \(n\) disks and you have moved \(n-1\) disks to peg B i.e. the Recursion Fairy has moved those \(n-1\) disks, after this you can move the \(n^{th}\) disk to peg C in one move and the rest of \(n-1\) disks onto peg C in one move (because of the restriction #3).

Consequently the recursion translates to the following equation \(T(n) = T(n-1) + 2 \thinspace \forall \thinspace n \geq 2 \) For the base case of when you have one disk, it only takes one move to move that one disk from any peg to any other. Solving this gives \(T(n) = 2n - 1 \thinspace \forall \thinspace n \geq 1 \)